Schedule
This talk is a mathematical primer for the rest of the
workshop. I define the basic notions that form the foundations of
higher-order Fourier analysis over finite fields, such as bias, Gowers
norm and polynomial rank. I will discuss the interrelationships between
these notions, regularity lemmas and show proofs of mini-results to
illustrate the theorems.
Higher-order Fourier analysis is a strong tool in the study of
analytic averages involving linear structures. One examines such
averages by replacing the involved functions by their Higher-order
Fourier expansion and reducing the problem to studying averages
involving bounded degree polynomials. However for this representation to
be useful, one often needs nice distributional/pseudorandomness
properties of the involved polynomials such as approximate orthogonality
or almost independence.
We will talk about regularity of polynomials which was
introduced by Green-Tao and Kauffman-Lovett in order to provide such
approximate orthogonalities. In most applications, however, one requires
stronger regularity properties of the polynomials. We will overview the
proof of such a strong near-orthogonality over arbitrary systems of
linear forms, and show as an application that this can be used to settle
a conjecture of Gowers and Wolf regarding the true complexity of
systems of linear forms.
The talk is based on a joint work with Hamed Hatami and Shachar Lovett.
12:35-14:00 Lunch break
Decomposition theorems proved by Gowers and Wolf provide an
appropriate notion of "Fourier transform" for higher-order Fourier
analysis. We will discuss some questions and techniques that arise from
trying to develop polynomial time algorithms for computing these
decompositions.
The original proofs for these theorems were non-constructive
and used the Hahn-Banach theorem. We will discuss constructive proofs
based on boosting which reduce the problem of computing these
decompositions to a certain kind of weak decoding for codes beyond the
list-decoding radius. We will also describe some special cases for which
such decodings are known to be possible, and the techniques which
achieve these.
Based on joint works with Arnab Bhattacharyya, Eli Ben-Sasson, Pooya Hatami, Noga Ron-Zewi and Julia Wolf.
Property testing aims for constant-query algorithms that
distinguish objects satisfying a predetermined property from objects
that are “far” from satisfying it. Along with the development of the
higher order Fourier analysis, there has been rapid progress in testing
affine-invariant properties of functions over a finite field, including
low-degree polynomials, and finally a characterization of
affine-invariant properties that are testable with a constant number of
queries was achieved. In this talk, we survey these results.
15:30-16:00 Coffee break
Let S and T be two dense subsets of Gn, where G is the special linear group SL(2,p) for a prime p congruent to 3 modulo 4. If you sample uniformly a tuple (s1,...,sn) from S and a tuple (t1,...,tn) from T then their interleaved product s1.t1.s2.t2...sn.tn is equal to any fixed g in G with probability (1 + |G|-Ω(n))/|G|.
Equivalently, the communication complexity of distinguishing tuples whose interleaved product is equal to g from those whose product is equal to a different g' is Ω(n log |G|),
even if the protocol is randomized and only achieves a small advantage
over random guessing. This result is tight and improves on the Ω(n) bound that follows by reduction from the inner product function.
Gowers (2007) and later Babai, Nikolov, and Pyber proved that if S, T, and U are dense subsets of a simple, non-abelian group G, then STU = g with probability (1/|G|)(1 + o(1)). For the special case of G = SL(2,p), this also follows from our result. Unlike previous proofs, ours does not rely on representation theory.
Joint work with Timothy Gowers.
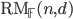 for a finite field
for a finite field 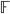 is defined by n-variate degree-d polynomials over
is defined by n-variate degree-d polynomials over 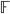 .
As far as we know, the list decoding radius of Reed- Muller codes can
be as large as the minimal distance of the code. This is known in a
number of cases: The Goldreich-Levin theorem and its extensions
established it for d = 1 (Hadamard codes); Gopalan, Klivans and Zuckerman established it for the binary field
.
As far as we know, the list decoding radius of Reed- Muller codes can
be as large as the minimal distance of the code. This is known in a
number of cases: The Goldreich-Levin theorem and its extensions
established it for d = 1 (Hadamard codes); Gopalan, Klivans and Zuckerman established it for the binary field 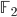 ; and Gopalan established it for d = 2
and all fields. In a recent work with Lovett, we prove the conjecture
for all constant prime fields and all constant degrees. The proof relies
on several new ingredients, including higher-order Fourier analysis.
; and Gopalan established it for d = 2
and all fields. In a recent work with Lovett, we prove the conjecture
for all constant prime fields and all constant degrees. The proof relies
on several new ingredients, including higher-order Fourier analysis.